We published a paper on it in Nucleic Acids Research in 2012: The Genome Portal of the Department of Energy.
-- a simple example of pig script to count kmers
1 register /.../biopig-core-0.3.0-job-pig.jar
2 A = load '$input' using gov.jgi.meta.pig.storage.FastaStorage as (id: chararray, d: int, seq: bytearray, header: chararray);
3 B = foreach A generate flatten(gov.jgi.meta.pig.eval.KmerGenerator(seq, 20)) as (kmer:bytearray);
4 C = group B by kmer parallel $p;
5 D = foreach C generate group, count(B);
6 E = group D by $1 parallel $p;
7 F = foreach E generate group, count(D);
8 store F into '$output';

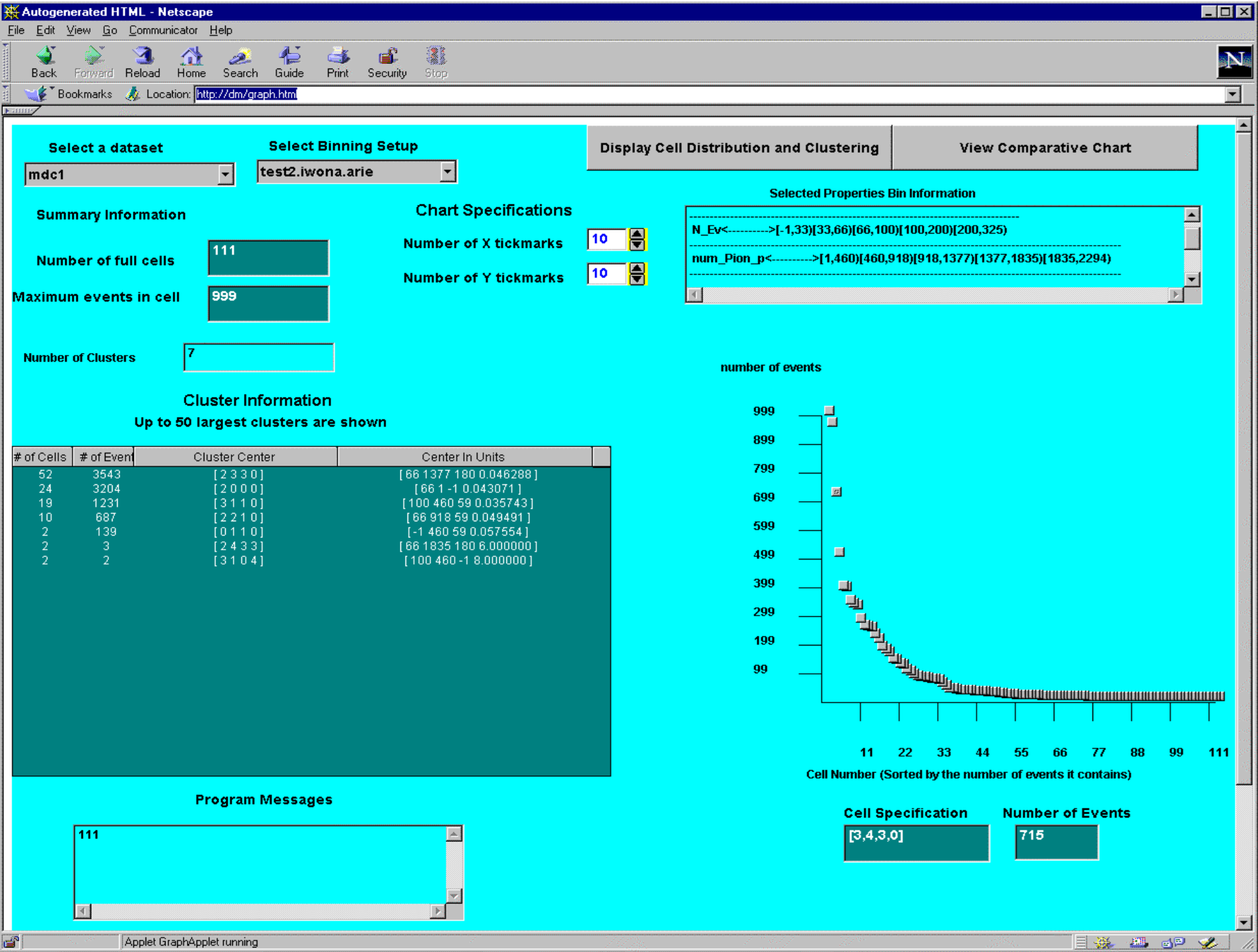
- Read the data (one pass) and populate the cells
- Sort the cells by the number of events
- Grow a cluster around the largest cell. Find all neighbors of Manhattan distance 1. Stop growing when events in a cell are below a threshold, or when the gradient increases.
- Then grow the cluster around the next available largest cell.
- Repeat until all cells are in a cluster
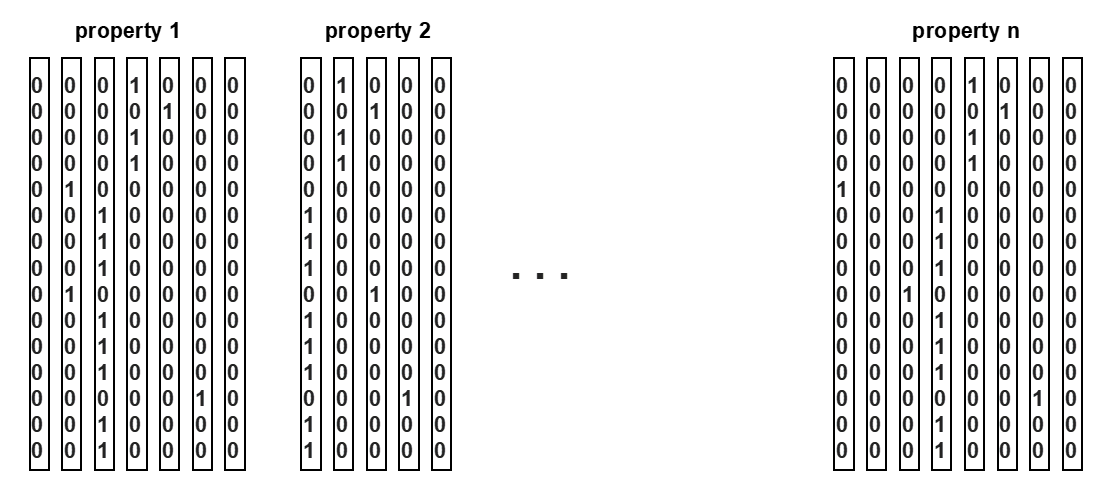
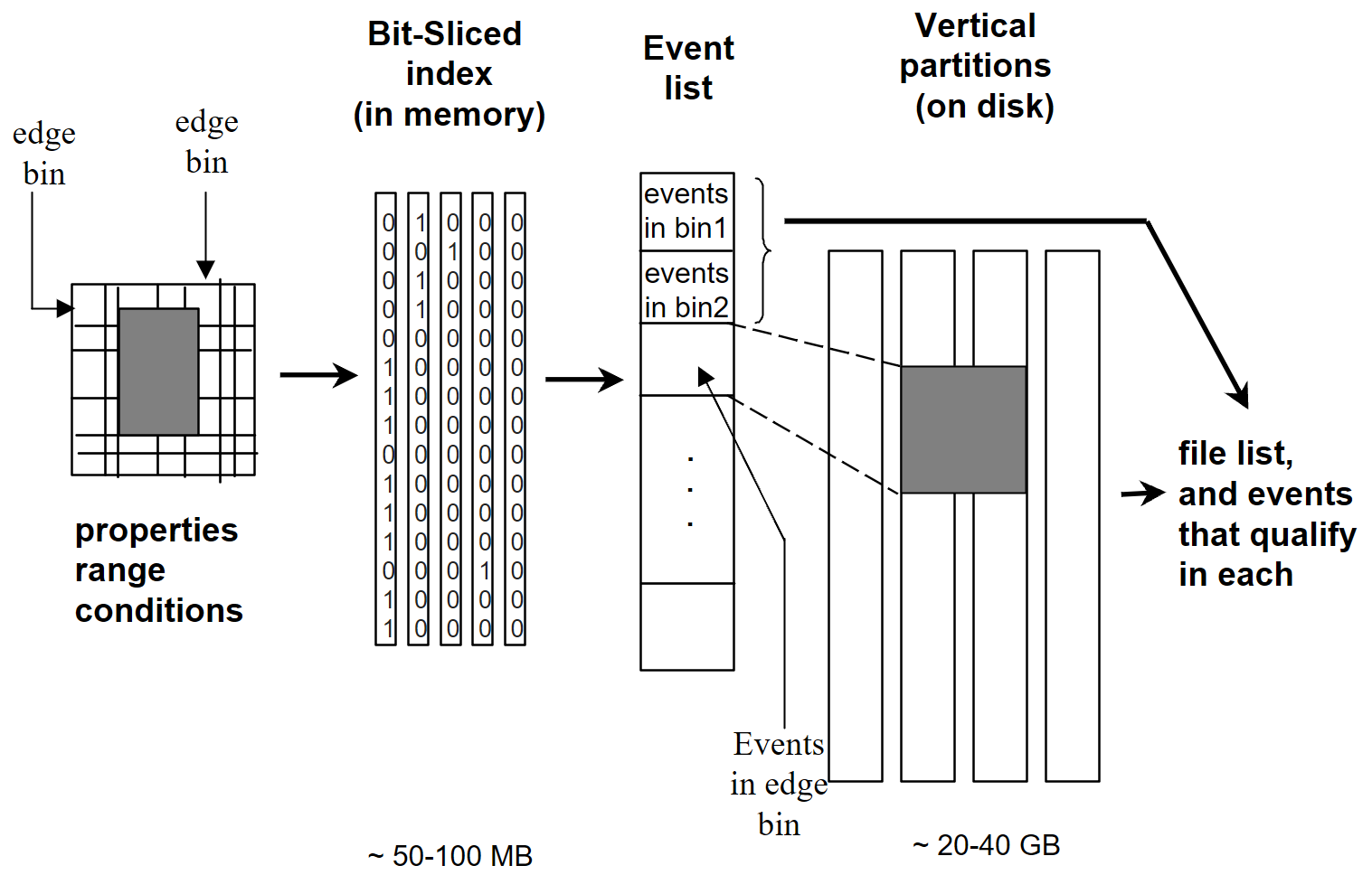
We now compress the vertical bit-vectors using a modified version of run-length encoding. The advantage of this scheme is that boolean operations can be performed directly on the compressed vectors without decompression. This scheme is particularly effective for highly skewed data such as High Energy Physics data. Our version of run-length encoding does not encode short sequences into counts. Instead, it represents them as-is. A single bit in each word indicates whether it is a count or a pattern. Results show a compression factor of 10-100. The choice of bins and bin boundaries has a significant impact on compression. Assume 100 properties, each with 10 bins. This requires 10¹¹ bits before compression. With a compression factor of 100, the space required is 10⁹ bits, or about 125 MBs. This can be stored permanently in memory. Note that it is not necessary to keep all bit slices in memory. Only the most relevant slices for a query need to be retained.
- The state ["0" or "1"] at the current position and the number of bits of the current run (number of consecutive bits of that same state), 'num', from each bit-slice, are extracted (decoded).
- The result is created (encoded) by performing the required logical operation (AND, OR, XOR) on the state bits from each bit-slice and subtracting the smaller 'num' from the larger and appending the result to the resulting bit-slice. The resulting bit-slice is encoded as we go along, using the most efficient method for the size of its run lengths.
function bmp_or( bitslice left,
bitslice right )
{
while( there_are_more_bits(left)
and there_are_more_bits(right) )
{
lbit = decode( left, lnum );
rbit = decode( right, rnum );
result_bit = lbit | rbit;
result_num = min( lnum, rnum );
lnum = lnum - result_num;
rnum = rnum - result_num;
encode( result,
result_bit,
result_num );
}
return result;
}

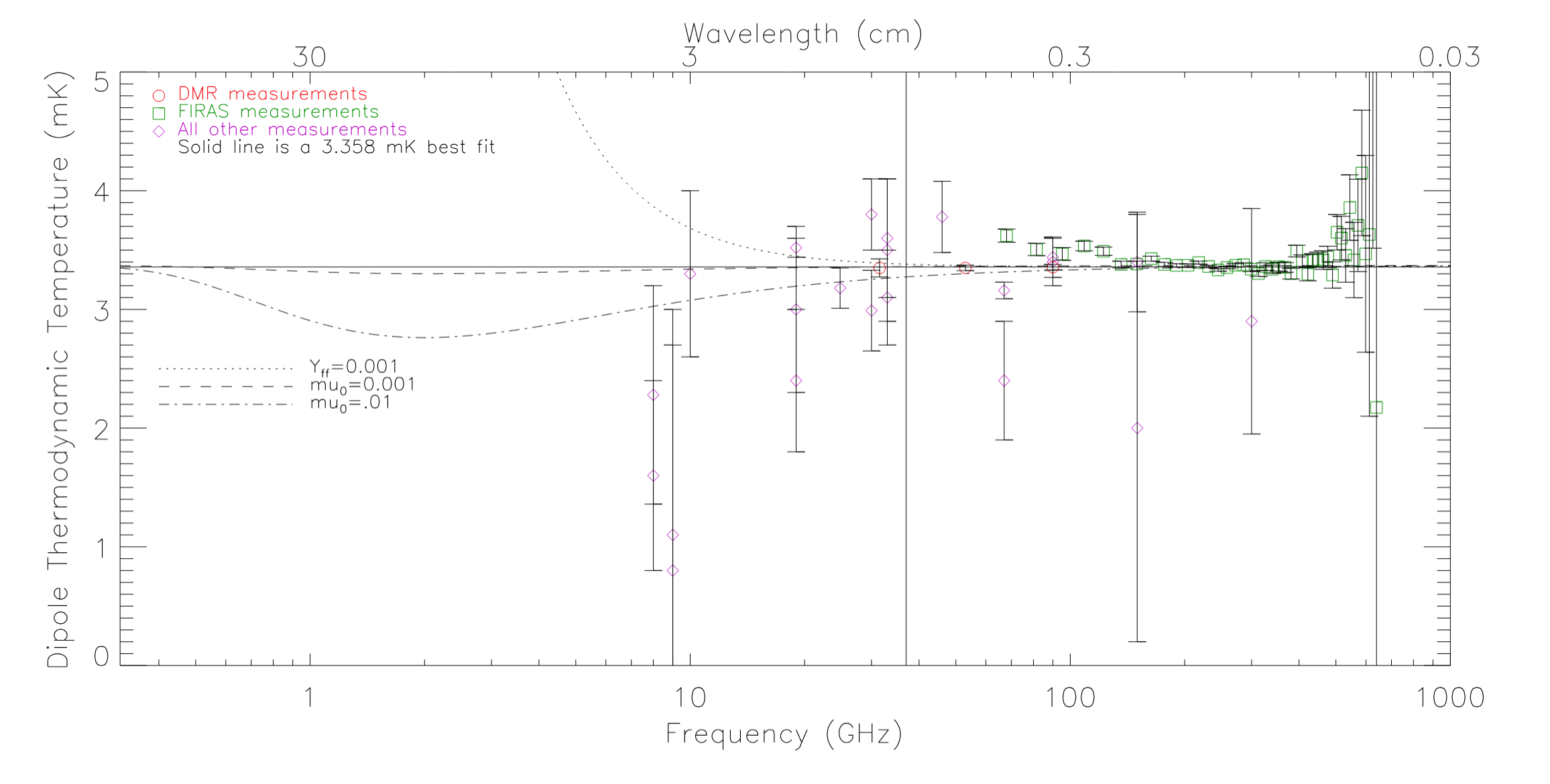
The Levenberg-Marquardt method is used to iterate to the optimal $\chi^2$. It combines the Steepest Decent and Grid Search methods into an algorithm with a fast convergence. By Taylor expansion of $\chi^2$ we have
$$\begin{multline*}\chi^2 = \chi^2(0)+\sum_i \frac{\partial \chi^2}{\partial x_i}x_i\\+\frac{1}{2}\sum_{i,j}\frac{\partial^2\chi^2}{\partial x_i\partial x_j}x_ix_j+...\end{multline*}$$which we can write as
$$\chi^2\approx \gamma - \vec{d}\cdot\vec{a}+{1\over 2}\vec{a}^T\cdot{\bf D}\cdot\vec{a} \tag{1}\label{eq:parabola}$$where $\vec{d}$ is a vector and ${\bf D}$ is a square matrix. This leads to
$$a_{\rm min}\approx a_{\rm cur}+{\bf D}^{-1}\cdot\left[-\nabla \chi^2(a_{\rm cur})\right] \tag{2}\label{eq:just_above}$$We measure $x_i$ and $s_i$. Our fitting function is $t(\vec{a})$.
$$\chi ^2 = \sum_{q,r}{\left\{ (s-t(\vec{a}))_q {\bf M}_{qr}^{-1} (s-t(\vec{a}))_r \right\}}$$ $${\partial \chi ^2 \over \partial a_i} = -2\sum_{q,r}{\left\{ \left({\partial t(\vec{a}) \over \partial a_i}\right)_q {\bf M}_{qr}^{-1} (s-t(\vec{a}))_r \right\}}$$Define
$$\beta_i\equiv -{1\over 2}{\partial \chi^2 \over \partial a_i}$$and
$$\alpha_{ij}\equiv {1\over 2}{\partial^2\chi^2 \over \partial a_i\partial a_j}$$We approximate $\alpha$ with [Press, W.H., et al. Numerical Recipes]
$$\alpha_{ij}\approx\sum_{q,r}\left\{ \left({\partial t(\vec{a}) \over \partial a_i}\right)_q {\bf M}_{qr}^{-1} \left({\partial t(\vec{a}) \over \partial a_j}\right)_r \right\}$$Following equation (\ref{eq:parabola}) we have ${\bf\alpha}={1\over 2} {\bf D}$ and we can re-write eq.~(\ref{eq:just_above}) as
$$\sum_i \alpha_{ij}\delta a_i=\beta_j$$Let
$$\delta a_i={1\over \lambda \alpha_{ii}}\beta_i,$$where $\lambda$ is a small positive constant and
$$\begin{aligned} \alpha_{ii}' &\equiv \alpha_{ii}(1+\lambda) \\ \alpha_{ij}' &\equiv \alpha_{ij}\;\;\;\;\;(i\neq j) \end{aligned}$$ $$\sum_i \alpha_{ij}'\delta a_i=\beta_j \tag{3}\label{eq:numrec14.4.14}$$The idea of the Levenberg-Marquardt method is summarized in the following procedure
- Compute $\chi^2(\vec{a})$.
- $\lambda \leftarrow 0.001$.
- Solve the linear equations (\ref{eq:numrec14.4.14}) for $\delta\vec{a}$ and evaluate $\chi^2(\vec{a}+\delta\vec{a})$.
- If $\chi^2(\vec{a}+\delta\vec{a})$ is smaller than a certain threshold, then stop.
- If $\chi^2(\vec{a}+\delta\vec{a})\geq\chi^2(\vec{a})$, increase $\lambda$ by a factor 10. Go to Step 3.
- If $\chi^2(\vec{a}+\delta\vec{a})<\chi^2(\vec{a})$, decrease $\lambda$ by a factor 10. Go to Step 3.
We also need to calculate the standard deviations, $\delta a_i$,
$${\bf C}={\bf{\alpha}}^{-1}$$and thus,
$$\delta a_i = \sqrt{\Delta \chi _\nu ^2}\sqrt{C_{ii}},$$where $\Delta \chi _\nu ^2$ is a change in $\chi ^2$ per degree of freedom corresponding to a change in one of the parameters $a_i$.
The Levenberg-Marquardt method was applied to the CMB datasets with great success. The method has several times more rapid convergence than the Steepest Descent and Grid Search methods. The latter two were tried first, but neither had reasonable convergence times, as they were implemented.
Sadly George passed away in 2025.

- Element Selection: Click the extension icon to activate, then hover over any element to see it highlighted
- Plain Text Copy: Click an element to copy its innerText (plain text content)
- HTML Copy Mode: Hold Shift while clicking to copy the element's innerHTML as rich HTML (with plain text fallback)
- Visual Feedback:
- Red outline for normal mode
- Blue outline for HTML mode (Shift held)
- Green outline after successful copy
- Keyboard Support: Press Escape to cancel selection mode